Understanding College Admissions Rates
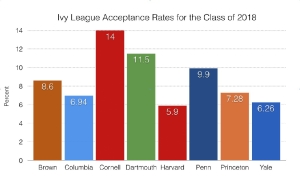“I figure Eric has a 6% chance of getting into Harvard.” Mr. Hennigan said in relation to his high school junior son at Guilford High School. Mr. Hennigan pointed to Harvard’s 5.9% admission rate as evidence.
Most people hate math. Statistics is a particularly arcane area of math but college admission strategy must be analyzed with some understanding of statistical models. In this case, 37, 307 applicants applied to Harvard in 2014. While true that 5.9% were admitted, this did not mean that Eric, a B plus student with low 600 SATs, decent but no extraordinary activities and no college admission hooks (legacy/VIP/athletic etc.) had a 5.9% chance of admission. I would put the odds somewhere between 0-1% with the exact decimal closer to 0. In providing college counseling to Connecticut students over the last decade, I have not seen a single student with Eric’s profile admitted to Harvard.
Why? Because while Harvard does get its fair share of college applicants willing to spend $70 on a college application and a few hours on college essays for a quixotic quest, the majority of applicants to Harvard have some combination of grades, test scores, numbers and/or college admission hooks that are stronger than Eric’s. In other words, most of the 94.1% rejected were superior candidates to Eric.
With that said, there is a positive way to use statistical modeling in relation to college admissions strategy. Given the right mix of colleges within the likely range of admission, students can and should apply to colleges that individually are possible but unlikely. So, for example, in Eric’s case, if he already had completed College Counseling Connecticut’s Core Six model of college admissions, then I still wouldn’t advise him to waste his time and money applying to Harvard. But, if he really wanted to give Boston College a shot, I would probably give the go-ahead, even though the odds of admission would still be low. (BC’s G.P.A/SAT numbers are distinctly higher than Eric’s.)
Statistical analysis provides a college admissions edge.